다이나믹 프로그래밍(Dynamic Programming)
동적 계획법이라고도 불리는 다이나믹 프로그래밍은 메모리를 약간 더 사용하여 수행 시간 효율성을 비약적으로 향상시키는 방법이다. 다이나믹 프로그래밍에서는 이미 계산된 결과(작은 문제)는 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 한다. 다이나믹 프로그래밍의 구현은 일반적으로 두 가지 방식(탑다운과 보텀업)으로 구성된다.
다이나믹 프로그래밍은 문제가 다음의 조건을 만족할 때 사용할 수 있다.
- 최적 부분 구조(Optimal Substructure)- 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있는 문제
- 중복되는 부분 문제(Overlapping Subproblem)- 동일한 작은 문제를 반복적으로 해결해야 하는 문제
※ 대표적인 다이나믹 프로그래밍 문제 - 피보나치 수열
- 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ... 같은 형태의 수열
- 피보나치 수열을 점화식으로 표현하면 다음과 같다.
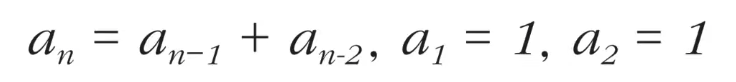
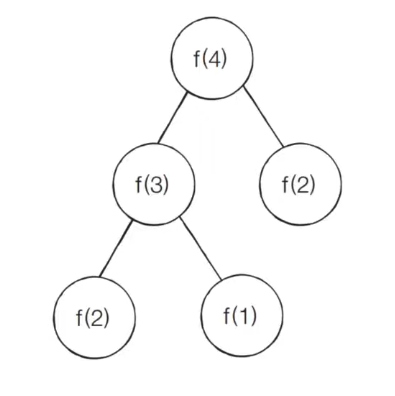
- n번째 피보나치 수를 f(n)이라 할 때 4번째 피보나치 수 f(4)를 구하는 과정은 다음과 같다.
# 피보나치 수열을 재귀 함수로 구현
def fibo(x):
if x == 1 or x == 2:
return 1
return fibo(n - 1) + fibo(n - 2)
print(fibo(4))재귀 함수를 이용하여 위의 수학적 점화식을 간단하게 구현할 수 있다. 하지만 이와 같이 작성하면 시간 복잡도가 O(2^N)이 되어 n이 커질수록 수행 시간이 기하급수적으로 늘어나는 문제가 생길 수 있다. 예로, f(30)을 계산하기 위해서 10억 가량의 연산이 필요하다.
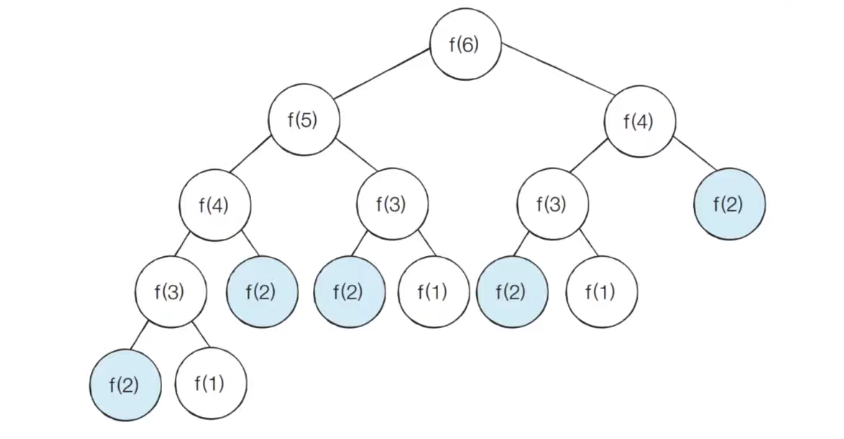
또한 위와 같이 중복되는 부분이 여러 번 호출되는 것을 확인할 수 있다.
피보나치 수열은 다이나믹 프로그래밍의 사용 조건을 둘 다 만족하므로 다이나믹 프로그래밍을 이용하여 효율적으로 구현할 수 있다.
다이나믹 프로그래밍 구현 방법
1. 탑다운(메모이제이션)
탑다운 방식은 하향식이라고도 하며 큰 문제를 해결하기 위해 작은 문제를 호출한다는 의미로 재귀 함수를 이용하여 구현한다. 이 과정에서 한 번 푼 문제의 값을 저장해 놓기 위해 메모이제이션 기법을 사용한다. 메모이제이션은 한 번 계산한 결과를 메모리 공간에 메모하는 기법으로 같은 문제를 다시 호출하면 메모했던 결과를 그대로 가져오는 방식이다. 값을 기록해 놓는다는 점에서 캐싱이라고도 한다.
# 탑다운 방식으로 피보나치 수열 구현
d = [0] * 100 # 메모이제이션을 위한 리스트 초기화
def fibo(x):
if x == 1 or x == 2:
return 1
if d[x] != 0: # 이미 계산한 적 있는 문제라면 그대로 반환
return d[x]
d[x] = fibo(x - 1) + fibo(x - 2) # 아니라면 점화식에 따라 결과 반환
return d[x]
print(fibo(99))
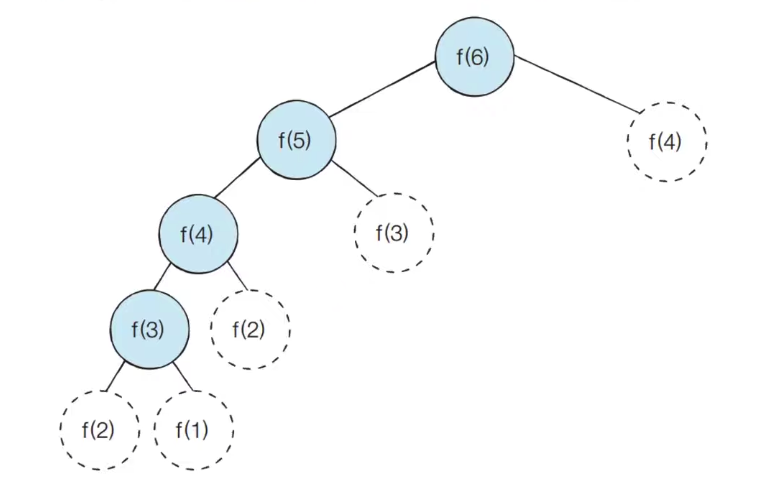
메모이제이션을 이용하는 경우 실제로 호출되는 함수는 색칠된 부분과 같으며 O(N)의 시간 복잡도를 갖는다.
2. 보텀업
보텀업 방식은 상향식이라고도 하며 반복문을 이용하여 작은 문제부터 차근차근 답을 도출해나가는 방식으로 다이나믹 프로그래밍의 전형적인 형태는 보텀업 방식이다. 보텀업 방식에서 결과 저장용 리스트는 DP 테이블이라고 부른다.
# 보텀업 방식으로 피보나치 수열 구현
d = [0] * 100 # DP 테이블 초기화
d[1] = 1
d[2] = 1
n = 99
for i in range(3, n + 1):
d[i] = d[i - 1] + d[i - 2]
print(d[n])
다이나믹 프로그래밍 VS 분할 정복
퀵 정렬 등에서 사용된 분할 정복과 다이나믹 프로그래밍은 둘 다 큰 문제를 작게 나눈다는 방식에서 문제가 최적 부분 구조를 가질 때 사용할 수 있다. 하지만 두 알고리즘의 차이는 부분 문제의 중복이다. 다이나믹 프로그래밍 문제에서는 각 부분 문제들이 서로 영향을 미치며 부분 문제가 중복 된다는 점이 특징이다. 반면에 분할 정복 문제에서는 동일한 부분 문제가 반복적으로 계산되지 않는다.
코딩 테스트에서의 다이나믹 프로그래밍
코딩 테스트에서의 다이나믹 프로그래밍 문제는 대체로 간단한 형태로 출제되어 대표적인 문제들만 바르게 습득해도 큰 어려움이 없을 것이다. 다이나믹 프로그래밍 유형임을 파악하는 방법은 먼저 특정한 문제를 그리디, 구현, 완전 탐색 등의 아이디어로 해결할 수 있는지 검토하는 것이다. 만약 다른 알고리즘으로 풀이 방법이 떠오르지 않는다면 또는 완전 탐색으로 너무 많은 수행 시간이 필요하다면 다이나믹 프로그래밍을 적용할 수 있는지 조건을 확인해보는 것이다. 일단 재귀 함수를 통해 비효율적인 프로그램을 작성한 뒤에 작은 문제에서 구한 답이 큰 문제에서 그대로 사용될 수 있으면, 즉 메모이제이션을 적용할 수 있으면 코드를 개선하는 방법도 좋은 아이디어다. 또한 가능하다면 재귀 함수를 이용하는 탑다운 방식보다는 보텀업 방식으로 구현하는 것이 더 낫다. 왜냐하면 시스템상 재귀 함수의 스택 크기가 한정되어 있을 수 있기 때문이다.
참고자료: 이것이 취업을 위한 코딩 테스트다 with 파이썬 - 나동빈 지음(한빛미디어)
'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| [알고리즘 이론] 최단 경로 알고리즘(2) - 플로이드 워셜 알고리즘 (0) | 2022.02.23 |
|---|---|
| [알고리즘 이론] 최단 경로 알고리즘(1) - 다익스트라 최단 경로 알고리즘 (0) | 2022.02.23 |
| [알고리즘 이론] 이진 탐색(Binaray Search) (0) | 2022.02.02 |
| [알고리즘 이론] 알고리즘 성능 평가 - 복잡도 (0) | 2022.01.25 |
| [알고리즘 이론] 정렬 알고리즘(Sorting Algorithm) (0) | 2022.01.24 |